COVIDCARE – Simpangan baku, atau yang sering disebut sebagai standar deviasi, adalah konsep dalam statistika yang digunakan untuk mengukur tingkat variasi atau seberapa dekat titik data dalam suatu kelompok.

Pada dasarnya, kita telah mempelajari konsep ini saat berada di sekolah menengah, dan kemudian mendalamkannya lebih lanjut di tingkat perguruan tinggi, terutama jika kita memilih ilmu statistik sebagai bidang studi utama.

Meskipun berita mengenai konsep ini terdengar rumit, sebenarnya cukup mudah dipahami.

Yang dibutuhkan adalah ketelitian dalam perhitungan dan pemahaman tentang bagaimana simpangan baku dapat membantu kita dalam menganalisis data.

Standar deviasi adalah alat yang berguna untuk mengukur sejauh mana data kita tersebar dalam kelompok, dan dapat memberikan wawasan penting dalam analisis statistik.

Contents show

Pengertian Simpangan Baku yang Perlu Kamu Ketahui!

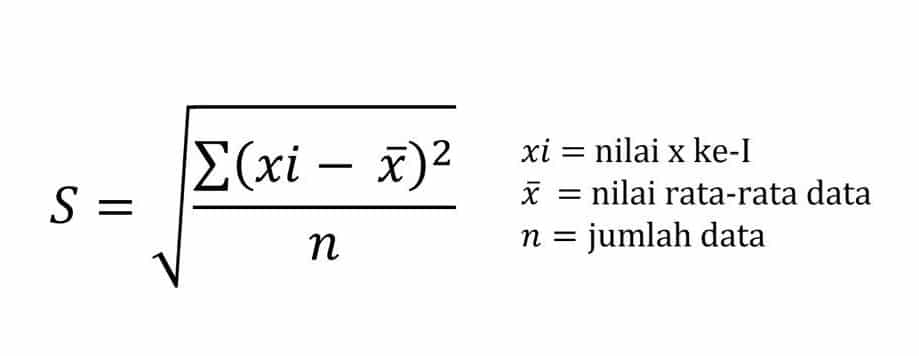
Simpangan baku, atau sering disebut standar deviasi, adalah konsep dalam statistika yang digunakan untuk mengukur seberapa seragam data dalam suatu kelompok.

Teknik ini juga berguna untuk menilai sejauh mana titik-titik data dalam sampel mendekati atau menjauhi nilai rata-rata (mean) dari sampel tersebut.

Sebelum memahami konsep ini, penting untuk memahami konsep nilai mean, median, dan modus dalam statistika.

Nilai simpangan baku dapat berupa angka nol, lebih kecil dari nol, atau lebih besar dari nol. Jika simpangan ini adalah nol, itu berarti semua nilai dalam kelompok data tersebut adalah sama.

Namun, jika simpangan ini lebih kecil atau lebih besar dari nol, itu menunjukkan bahwa titik-titik data individu memiliki perbedaan yang signifikan dari nilai rata-ratanya.

Dalam hal ini, semakin dekat titik data individu ke nilai rata-rata, semakin kecil simpangannya, yang berarti data cenderung homogen.

Sebaliknya, jika titik data berada jauh dari nilai rata-ratanya, simpangannya akan semakin besar. Oleh karena itu, memahami nilai rata-rata (mean) dalam data tunggal atau kelompok sangat penting dalam mengukur dan menganalisis simpangan baku.

Fungsi Dari Simpangan Baku dari Data

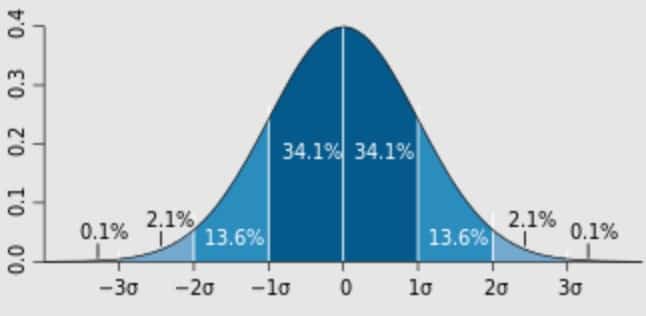
Simpangan baku memiliki peran penting dalam dunia statistika dan analisis data. Berikut adalah beberapa fungsi utama dari simpangan baku:

Mengukur Variabilitas

Simpangan baku digunakan untuk mengukur tingkat variasi atau sebaran data dalam suatu sampel atau populasi.

Ini membantu kita memahami sejauh mana data tersebar dari nilai rata-rata. Semakin besar simpangannya, semakin besar variasi data.

Mengukur Ketelitian

Simpangan baku membantu kita menilai ketelitian atau akurasi data. Jika simpangan kecil, data cenderung lebih dekat dengan nilai rata-rata, yang menunjukkan tingkat ketelitian yang tinggi.

Perbandingan

Dalam analisis statistik, simpangan baku digunakan untuk membandingkan kelompok data yang berbeda. Ini memungkinkan kita untuk menentukan apakah perbedaan antara kelompok data tersebut signifikan atau tidak.

Menentukan Distribusi Data

Simpangan baku membantu mengidentifikasi sejauh mana data mengikuti distribusi normal atau apakah ada outlier (nilai ekstrem) dalam data.

Keputusan Pengambilan Sampel

Dalam pengambilan sampel, simpangan baku digunakan untuk menentukan ukuran sampel yang diperlukan untuk mewakili populasi dengan tingkat kepercayaan tertentu. Semakin besar simpangan baku, semakin besar ukuran sampel yang diperlukan.

Jadi, simpangan ini memiliki peran yang penting dalam menganalisis data, membuat keputusan berdasarkan data, dan mengukur seberapa baik sampel mewakili populasi.

Meskipun perhitungan simpangan ini mungkin terlihat rumit, namun nilai dan pemahaman tentang simpangan baku membantu dalam pengambilan keputusan yang lebih baik dalam berbagai bidang, termasuk riset dan bisnis.

Rumus Simpangan Baku yang Perlu Kamu Ingat!

Simpangan memiliki beberapa rumus yang digunakan tergantung pada jenis data yang sedang dianalisis. Berikut adalah beberapa rumus simpangan yang umum digunakan:

Simpangan untuk Data Tunggal

Simpangan (S) untuk data tunggal dapat dihitung dengan rumus: S = √(Σ(xi – x)² / n) Keterangan:

S = simpangan bentuk baku
xi = nilai data ke-i
x = nilai rata-rata data
n = jumlah data

Simpangan untuk Data Berkelompok

Simpangan (S) untuk data berkelompok dapat dihitung dengan rumus: S = √(Σ(fi * (xi – x)²) / n) Keterangan:

S = simpangan bentuk baku
fi = frekuensi kelompok
xi = nilai tengah kelompok data ke-i
x = nilai rata-rata data
n = jumlah data

Simpangan untuk Data Sampel

Simpangan (S) untuk data sampel dapat dihitung dengan rumus: S = √(Σ(xi – x)² / (n-1)) Keterangan:

S = simpangan bentuk baku
xi = nilai data ke-i
x = nilai rata-rata data
n = jumlah data

Nilai Varian

Nilai varian (S^2) dapat dihitung dengan rumus: S^2 = Σ(xi²) – (Σxi)² / (n(n-1)) atau S^2 = Σ(xi – x)² / (n(n-1)) Keterangan:

S^2 = nilai varian
xi = nilai data ke-i
x = nilai rata-rata data
n = jumlah data

Standar Deviasi

Standar deviasi (S) dapat dihitung dengan rumus: S = √(Σ(xi²) – (Σxi)² / (n(n-1))) atau S = √(Σ(xi – x)² / (n(n-1))) Keterangan:

S = standar deviasi
xi = nilai data ke-i
x = nilai rata-rata data
n = jumlah data

Rumus-rumus ini digunakan untuk mengukur sebaran dan dispersi data, serta untuk mengevaluasi tingkat variasi dalam suatu dataset.

Cara Untuk Mencari Nilai Simpangan

Untuk menghitung nilai simpangan ini, teman-teman COVIDCARE dapat mengikuti langkah-langkah berikut:

Hitung Nilai Rata-Rata

Mulailah dengan menjumlahkan semua data yang ada dalam himpunan.
Bagi jumlah tersebut dengan jumlah data dalam himpunan untuk mendapatkan nilai rata-rata (mean).

Hitung Penyimpangan Tiap Data

Selanjutnya, hitung penyimpangan setiap titik data dengan cara mengurangkan nilai rata-rata dari setiap titik data.

Kuadratkan Penyimpangan

Kuadratkan masing-masing penyimpangan yang telah dihitung pada langkah sebelumnya.

Hitung Nilai Varian

Hitung nilai varian dengan menjumlahkan semua nilai kuadrat penyimpangan, kemudian bagi hasilnya dengan jumlah total data. Rumusnya adalah: S^2 = Σ(xi – x)² / n

Hitung Standar Deviasi

Akhirnya, hitung standar deviasi dengan mengambil akar kuadrat dari nilai varian. Rumusnya adalah: S = √S^2

Dengan mengikuti langkah-langkah ini, kamu akan mendapatkan nilai simpangan baku atau standar deviasi dari data yang kamu analisis. Ini membantu dalam mengukur sebaran data dan tingkat variasi dalam himpunan data tersebut.

Contoh Soal Simpangan Baku + Cara Penyelesaiannya

Contoh Soal 1: Simpangan Baku Data Tunggal

Sebuah toko pakaian mencatat penjualan harian selama 5 hari (dalam ribuan rupiah) sebagai berikut: 8, 9, 10, 12, dan 11. Hitunglah simpangan baku dari data penjualan ini.

Jawaban 1:

Langkah 1: Hitunglah rata-rata dari data tersebut.

Rata-rata (x̄) = (8 + 9 + 10 + 12 + 11) / 5 = 50 / 5 = 10 ribuan rupiah.

Langkah 2: Hitung penyimpangan setiap data dari rata-rata, kuadratkan, dan jumlahkan.

Penyimpangan pertama = 8 – 10 = -2 ribuan rupiah
Penyimpangan kedua = 9 – 10 = -1 ribuan rupiah
Penyimpangan ketiga = 10 – 10 = 0 ribuan rupiah
Penyimpangan keempat = 12 – 10 = 2 ribuan rupiah
Penyimpangan kelima = 11 – 10 = 1 ribuan rupiah

Jumlah kuadrat penyimpangan = (-2)^2 + (-1)^2 + (0)^2 + (2)^2 + (1)^2 = 4 + 1 + 0 + 4 + 1 = 10 ribuan rupiah.

Langkah 3: Hitung varian.

Varian (S^2) = Jumlah kuadrat penyimpangan / jumlah data = 10 / 5 = 2 ribuan rupiah.

Langkah 4: Hitung standar deviasi.

Standar deviasi (S) = √Varian = √2 ribuan rupiah ≈ 1.41 ribuan rupiah.

Jadi, simpangan baku dari data penjualan harian toko pakaian adalah sekitar 1.41 ribuan rupiah.

Contoh Soal 2: Simpangan Baku Data Kelompok

Data berikut ini menunjukkan jumlah buku yang dibaca oleh sekelompok siswa selama satu bulan:

Jumlah Buku (dalam puluhan)	Jumlah Siswa
2	3
3	6
4	8
5	5
6	4

Hitunglah simpangan baku dari data ini.

Jawaban 2:

Langkah 1: Hitung rata-rata data dengan memperhitungkan frekuensi.

Rata-rata (x̄) = (23 + 36 + 48 + 55 + 6*4) / (3 + 6 + 8 + 5 + 4) = (6 + 18 + 32 + 25 + 24) / 26 = 105 / 26 ≈ 4.038 buku.

Langkah 2: Hitung penyimpangan setiap nilai dari rata-rata, kuadratkan, dan jumlahkan.

Penyimpangan pertama = 2 – 4.038 ≈ -2.038
Penyimpangan kedua = 3 – 4.038 ≈ -1.038
Penyimpangan ketiga = 4 – 4.038 ≈ -0.038
Penyimpangan keempat = 5 – 4.038 ≈ 0.962
Penyimpangan kelima = 6 – 4.038 ≈ 1.962

Jumlah kuadrat penyimpangan ≈ (-2.038)^2 + (-1.038)^2 + (-0.038)^2 + (0.962)^2 + (1.962)^2 ≈ 8.196 buku^2.

Langkah 3: Hitung varian.

Varian (S^2) = Jumlah kuadrat penyimpangan / jumlah total siswa – 1 = 8.196 / (26 – 1) = 8.196 / 25 ≈ 0.32864 buku^2.

Langkah 4: Hitung standar deviasi.

Standar deviasi (S) ≈ √Varian ≈ √0.32864 buku^2 ≈ 0.573 buku.

Jadi, simpangan baku dari data jumlah buku yang dibaca oleh siswa selama satu bulan adalah sekitar 0.573 buku.

Itulah penjelasan lengkap mengenai simpangan baku dari COVIDCARE mudah-mudahan apa yang kami sampaikan ini membantu kamu ya!

Baca juga: