COVIDCARE – Dalam ilmu Matematika yang luas, terdapat dua konsep penting yang saling terkait, yaitu barisan aritmatika dan deret aritmatika.

Kedua konsep ini membawa kita ke dalam dunia operasi dasar bilangan seperti pembagian, perkalian, pengurangan, dan penjumlahan. Namun, dalam kesempatan ini, mari kita fokus pada pemahaman tentang barisan aritmatika.

Barisan aritmatika adalah urutan bilangan yang setiap elemennya memiliki hubungan aritmatika dengan elemen sebelumnya. Hubungan ini dapat dinyatakan dengan suatu selisih yang konstan.

Dengan kata lain, setiap anggota dalam barisan aritmatika dapat ditemukan dengan menambahkan selisih yang sama ke elemen sebelumnya.

Misalnya, jika kita memiliki barisan dengan elemen pertama (a_1) dan selisih (d), maka elemen-elemen berikutnya dalam barisan tersebut dapat dinyatakan sebagai berikut:

(a_2 = a_1 + d)
(a_3 = a_2 + d = a_1 + 2d)
(a_4 = a_3 + d = a_1 + 3d)

Contoh umum dari barisan aritmatika adalah barisan bilangan bulat genap (2, 4, 6, 8, …) di mana selisih antara setiap anggota adalah 2.

Barisan aritmatika memiliki banyak aplikasi dalam berbagai aspek kehidupan, terutama dalam ilmu Matematika dan ilmu pengetahuan lainnya.

Ini membantu kita dalam memodelkan pola-pola yang terjadi secara berulang, menghitung jumlah total elemen-elemen dalam barisan tersebut (yang merupakan dasar dari deret aritmatika), dan banyak lagi.

Jadi, secara singkat, barisan aritmatika adalah urutan bilangan di mana setiap elemennya memiliki hubungan aritmatika dengan elemen sebelumnya melalui suatu selisih konstan.

Ini adalah konsep yang penting dan bermanfaat dalam Matematika. Dan untuk lebnih jelasnya silahkan simak berita ini sampai selesai ya.

Contents show

Pengertian Barisan Aritmatika

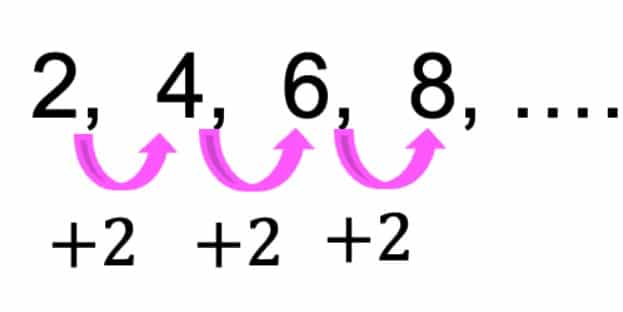
Barisan aritmatika, dalam pengertiannya yang singkat, merujuk pada urutan bilangan yang menunjukkan pola yang konsisten. Pola ini dapat muncul sebagai hasil dari operasi pengurangan atau penjumlahan.

Dalam konteks ini, setiap elemen dalam urutan bilangan memiliki selisih yang tetap di antara mereka, yang sering disebut sebagai “beda” dan biasanya dilambangkan dengan huruf “b.”

Untuk memberikan pemahaman lebih lanjut, mari kita ambil contoh barisan aritmatika berikut:

Suku pertama dalam barisan ini adalah angka 2, yang sering disimbolkan sebagai U1 atau secara matematis dilambangkan sebagai “a.”
Suku kedua adalah angka 5, yang umumnya disimbolkan sebagai U2.
Suku ketiga adalah angka 8, yang biasanya disimbolkan sebagai U3, dan seterusnya.

Dalam contoh di atas, barisan aritmatika berurutan adalah 2, 5, dan 8. Jika kita melihat angka-angka ini, kita dapat menyimpulkan bahwa antara angka 2 dan 5 terdapat selisih 3 angka.

Begitu juga, antara angka 5 dan 8 terdapat selisih yang sama, yaitu 3 angka. Ini menunjukkan bahwa barisan aritmatika ini memiliki selisih yang konstan, yang dalam hal ini adalah 3.

Dengan demikian, setiap suku berikutnya dalam barisan ini dapat ditemukan dengan menambahkan 3 ke suku sebelumnya.

Barisan aritmatika adalah konsep yang penting dalam matematika dan memiliki berbagai aplikasi dalam pemodelan pola, perhitungan jumlah total elemen-elemen dalam barisan (yang merujuk pada deret aritmatika), dan banyak aspek lainnya dalam dunia matematika.

Jenis-Jenis Barisan Aritmatika

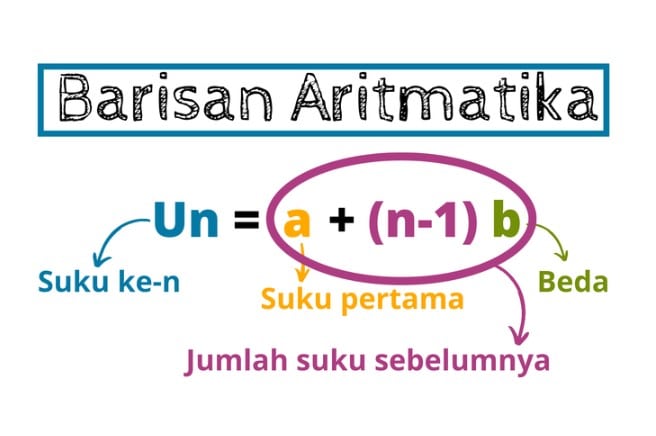
Barisan aritmatika memiliki dua jenis utama, yaitu barisan naik dan barisan turun, yang membedakan arah perubahan nilai bilangan dalam barisan tersebut.

Perlu dicatat bahwa ciri utama yang membedakan keduanya adalah nilai beda (b) antara setiap dua suku berturut-turut dalam barisan.

Barisan Naik

Barisan naik adalah tipe barisan aritmatika di mana nilai beda (b) antara setiap dua suku berturut-turut adalah positif. Dengan kata lain, nilai suku-suku berikutnya dalam barisan ini akan lebih besar dari suku sebelumnya.

Sebagai contoh, pertimbangkan barisan berikut: 7, 14, 21, 28, 35. Dalam barisan ini, selisih antara setiap dua suku berturut-turut adalah 7.

Oleh karena itu, barisan ini termasuk dalam kategori barisan naik. Setiap suku selanjutnya akan memiliki nilai yang lebih tinggi daripada suku sebelumnya.

Barisan Turun

Barisan turun adalah tipe barisan aritmatika di mana nilai beda (b) antara setiap dua suku berturut-turut adalah negatif. Ini berarti bahwa nilai suku-suku berikutnya dalam barisan ini akan lebih kecil dari suku sebelumnya.

Sebagai contoh, pertimbangkan barisan berikut: 45, 40, 35, 30. Dalam barisan ini, selisih antara setiap dua suku berturut-turut adalah -5.

Oleh karena itu, barisan ini masuk dalam kategori barisan turun. Setiap suku selanjutnya akan memiliki nilai yang lebih rendah daripada suku sebelumnya.

Dengan demikian, perbedaan utama antara barisan naik dan barisan turun adalah arah perubahan nilai suku-suku dalam barisan, yang ditentukan oleh tanda positif (naik) atau negatif (turun) dari nilai beda (b).

Konsep ini membantu kita memahami karakteristik dasar dari berbagai jenis barisan aritmatika.

Rumus Barisan Aritmatika dan Contoh Soal Barisan Aritmatika Tingkat Mudah

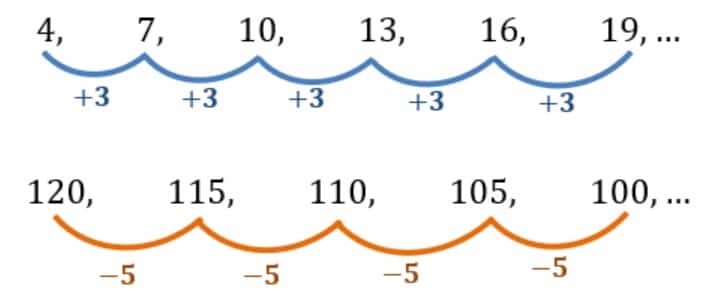
Rumus Barisan Aritmatika adalah alat yang sangat berguna ketika kita harus mencari suku-suku dalam sebuah barisan dengan cepat.

Barisan aritmatika adalah urutan angka yang memiliki pola pertambahan atau pengurangan yang tetap antar suku-sukunya.

Rumus Barisan Aritmatika:

Untuk mencari suku ke-n (Un):
Un = U1 + (n – 1) * b
Untuk mencari nilai beda (b):
b = Un – Un-1

Dalam rumus tersebut:

Un adalah suku ke-n yang ingin dicari.
U1 adalah suku pertama dalam barisan (a).
n adalah urutan suku yang ingin dicari.
b adalah nilai beda antara suku-suku dalam barisan.

Contoh Soal Barisan Aritmatika Tingkat Mudah: Misalkan kita memiliki barisan aritmatika sebagai berikut: 3, 7, 11, 15, …

Kita ingin mencari suku ke-10 dalam barisan tersebut (Un).

Langkah 1: Tentukan nilai U1 (suku pertama) dan nilai b (beda).

U1 = 3
Dengan melihat pola, kita dapat menghitung beda (b) dengan mengurangkan suku kedua (U2) dengan suku pertama (U1).
b = U2 – U1 = 7 – 3 = 4

Langkah 2: Gunakan rumus untuk mencari suku ke-10 (Un).

n = 10 (kita ingin mencari suku ke-10).
Un = U1 + (n – 1) * b
Un = 3 + (10 – 1) * 4
Un = 3 + 9 * 4
Un = 3 + 36
Un = 39

Jadi, suku ke-10 dalam barisan aritmatika ini adalah 39.

Dengan menggunakan rumus barisan aritmatika, kita dapat dengan mudah mencari suku-suku dalam barisan tersebut tanpa harus menghitung satu per satu.

Rumus ini sangat bermanfaat dalam pemecahan masalah matematika yang melibatkan barisan aritmatika.

Rumus Cepat Mencari Suku ke-n dan Beda Barisan Aritmatika

Kadang-kadang, soal-soal yang kita hadapi dalam barisan aritmatika bisa menjadi lebih rumit. Suku pertama (a) dan beda (b) tidak selalu diberikan.

Bagaimana cara kita menyelesaikan soal semacam ini? Untungnya, ada rumus cepat yang bisa digunakan untuk mempercepat perhitungan. Jadi COVIDCARE akan membagikan rumusnya di bawah ini ya.

Rumus Cepat untuk Mencari Suku ke-n (Un)

Jika kita tahu beberapa suku dalam barisan (Un1, Un2, dan seterusnya) dan nilai n untuk suku yang ingin kita cari (ni), kita bisa menggunakan rumus berikut: ni = Uni – Un1 + (n1 * b) * b Dalam rumus ini:

Un1 adalah suku yang kita tahu (biasanya suku pertama yang diketahui).
Un2 adalah suku lain yang kita tahu (biasanya suku ke-dua yang diketahui).
ni adalah suku yang ingin kita cari.
n1 adalah urutan suku yang diberikan (biasanya urutan suku pertama yang diketahui).
b adalah beda atau selisih antar suku-suku dalam barisan.

Rumus Cepat untuk Mencari Beda (b)

Jika kita tahu beberapa suku dalam barisan (Un1, Un2, dan seterusnya) dan nilai n1 dan n2 untuk suku-suku yang diketahui, kita bisa menggunakan rumus berikut untuk mencari beda (b): b = (Un2 – Un1) / (n2 – n1) Dalam rumus ini:

Un1 adalah suku pertama yang diketahui.
Un2 adalah suku lain yang diketahui.
n1 adalah urutan suku pertama yang diketahui.
n2 adalah urutan suku lain yang diketahui.
b adalah beda atau selisih antar suku-suku dalam barisan.

Dengan rumus-rumus cepat ini, bahkan jika kita hanya memiliki beberapa informasi tentang suku-suku dalam barisan, kita dapat dengan cepat mencari suku yang ingin kita temukan.

Cara Mencari Suku Pertama Barisan Aritmatika

Terkadang, kita juga diminta untuk menentukan suku pertama (a) dalam barisan aritmatika. Untuk melakukan ini, kita dapat menggunakan informasi tentang suku-suku lain dalam barisan.

Contoh Soal 1: Jika suku keempat adalah 55, suku ketujuh adalah 85, dan beda dalam barisan tersebut adalah 10, berapakah suku pertamanya?

Langkah 1: Menyusun Persamaan dari Suku-suku yang Diketahui

Untuk suku keempat (n = 4):
Un4 = a + (4 – 1) * b = 55
Untuk suku ketujuh (n = 7):
Un7 = a + (7 – 1) * b = 85

Langkah 2: Menyelesaikan Sistem Persamaan Linear

Dengan menggunakan metode substitusi atau eliminasi, kita dapat menyelesaikan sistem persamaan di atas untuk menemukan nilai a (suku pertama).

Langkah 3: Substitusi Nilai a ke dalam Persamaan

Setelah menemukan nilai a, kita dapat mengonfirmasi nilai a dengan memasukkannya kembali ke salah satu persamaan di atas dan memastikan bahwa persamaan tersebut masih berlaku.

Dengan demikian, kita dapat menemukan nilai suku pertama (a) dalam barisan aritmatika.

Contoh Soal 2: Jika suku kelima adalah 27 dan suku kesembilan adalah 39, tentukan suku pertama dari barisan tersebut.

Dalam soal ini, kita tidak tahu nilai beda (b), tetapi kita memiliki suku-suku lain dalam barisan. Kita dapat menggunakan langkah-langkah yang sama untuk menentukan suku pertama (a).

Dengan memahami rumus-rumus ini, kita dapat dengan mudah menyelesaikan berbagai jenis soal yang melibatkan barisan aritmatika.

Dalam beberapa kasus, kita mungkin perlu menggunakan rumus cepat atau sistem persamaan linear, tetapi dengan latihan, kita akan menjadi lebih terampil dalam menyelesaikan masalah semacam itu.

Barisan Aritmatika Bertingkat: Konsep dan Contoh

Barisan aritmatika bertingkat adalah jenis barisan di mana nilai beda tetapnya tidak dapat langsung ditemukan pada tingkat pertama. Sebaliknya, nilai beda ini harus dicari pada tingkat-tingkat berikutnya.

Pada barisan bertingkat ini, ada banyak tingkatan yang dapat mencapai tingkat sepuluh atau lebih.

Secara umum, kita dapat mengidentifikasi berapa tingkat dalam sebuah barisan berdasarkan di mana nilai beda tetapnya ditemukan. Jika nilai beda tetap ditemukan pada tingkat pertama, barisan tersebut disebut barisan bertingkat satu.

Sebaliknya, jika nilai beda tetap ditemukan pada tingkat kedua, barisan tersebut disebut barisan bertingkat dua, dan seterusnya. Untuk memahaminya lebih baik, mari kita lihat contohnya.

Misalnya kita memiliki barisan bilangan: 1, 5, 12, 22, 35, … Pada barisan ini, tidak terlihat nilai beda tetapnya pada tingkat pertama. Untuk mencari nilai beda, kita perlu melihat perbedaan antara suku-suku berurutan.

Misalnya, dari 1 ke 5, perbedaannya adalah 4; dari 5 ke 12, perbedaannya adalah 7; dari 12 ke 22, perbedaannya adalah 10; dan dari 22 ke 35, perbedaannya adalah 13.

Jadi, barisan ini dengan nilai beda yang telah kita temukan akan seperti ini:

1, 5, 12, 22, 35

4 7 10 13

Sekarang, jika kita anggap angka 4, 7, 10, dan 13 di atas sebagai barisan baru, kita dapat melihat bahwa perbedaan antara suku pertama dan kedua, suku kedua dan ketiga, dan seterusnya adalah nilai yang tetap, yaitu 3. Sehingga, barisan ini akan terlihat seperti ini:

1, 5, 12, 22, 35

4 7 10 13

3 3 3

Dalam contoh ini, angka 4, 7, 10, dan 13 dapat dianggap sebagai barisan tingkat pertama, dan kemudian suku-suku baru yang ditemukan dari selisih barisan sebelumnya dapat dianggap sebagai barisan tingkat kedua. Nilai beda tetap ditemukan pada tingkat kedua.

Mempelajari barisan aritmatika pada pandangan pertama mungkin terlihat rumit, tetapi jika kita memahami konsep dasarnya dan menguasai rumus-rumusnya, maka topik ini tidak akan menjadi masalah.

Untuk meningkatkan pemahaman dan keterampilan, berlatihlah mengerjakan berbagai soal terkait barisan aritmatika secara berkala ya teman-teman COVIDCARE.

Baca juga: