COVIDCARE – Dalam perjalanan memahami ilmu matematika, salah satu aspek yang tak dapat dihindari adalah pembelajaran tentang bilangan berpangkat.

Pengetahuan ini menjadi pondasi utama yang akan mendukung pemahaman dalam bab-bab matematika yang lebih kompleks di masa depan.

Dari menyelesaikan persamaan matematika hingga membantu melakukan perhitungan yang melibatkan angka-angka besar dengan cepat, konsep eksponen menjadi alat yang sangat penting.

Itulah mengapa pemahaman tentang eksponen menjadi bagian integral dari kurikulum pendidikan di sekolah.

Selain menjadi kunci untuk memecahkan berbagai masalah matematika, bilangan pangkat juga memiliki sifat-sifat yang unik dan penting untuk dipahami.

Pengetahuan tentang sifat-sifat ini akan membantu mempermudah manipulasi dan perhitungan yang melibatkan eksponen.

Mari kita simak berita lebih dalam dunia bilangan pangkat, jelajahi berbagai sifatnya, dan temukan contoh soal yang mendalam beserta jawabannya. Pemahaman yang kuat tentang eksponen akan membuka pintu keajaiban matematika yang lebih besar.

Contents show

Apa Itu Bilangan Pangkat atau Eksponen

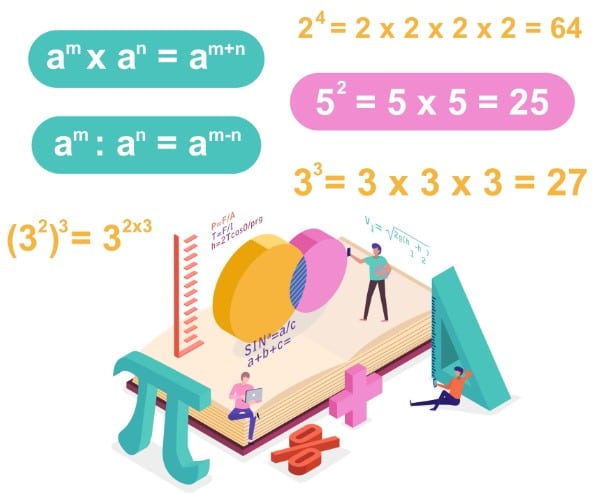
Bilangan pangkat atau eksponen adalah konsep matematika yang sederhana namun memiliki dampak yang sangat besar dalam berbagai aspek kehidupan.

Pada dasarnya, bilangan pangkat menggambarkan perkalian berulang kali dengan bilangan yang sama, sebanyak pangkat yang ditunjukkan. Mari kita menjelajahi konsep ini dengan lebih dalam.

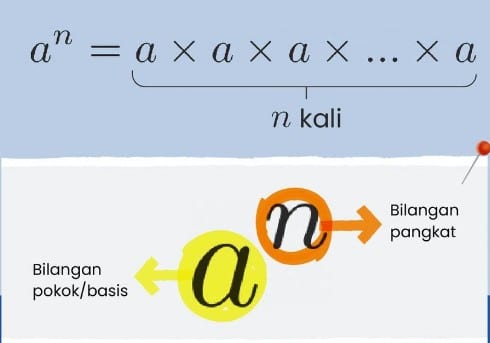
Dalam notasi sederhana, bilangan pangkat ditunjukkan dengan menggunakan dua faktor utama: dasar (a) dan pangkat (n). Bilangan pangkat ini dapat diilustrasikan sebagai berikut:

an = a x a x a x a x … x a

Contohnya, jika kita memiliki angka 2 yang dikalikan dengan dirinya sendiri sebanyak 4 kali, maka hasilnya adalah 2x2x2x2, yang juga bisa ditulis sebagai 2 pangkat 4 (2^4).

Namun, perlu diingat bahwa notasi ini umumnya berlaku untuk pangkat yang positif. Bagaimana jika pangkatnya berbentuk pecahan, akar, atau bahkan bernilai negatif? Inilah saatnya untuk menjelajahi berbagai sifat yang dimiliki oleh bilangan pangkat.

Bilangan pangkat bukan sekadar konsep matematika, tetapi juga menjadi alat penting dalam berbagai bidang ilmu.

Misalnya, dalam fisika, kita dapat menggambarkan kecepatan cahaya yang sangat besar (300.000.000 meter per detik) dengan notasi yang lebih sederhana, yaitu 3 x 10^8.

Dengan pemahaman tentang sifat-sifat bilangan pangkat, kita dapat menggali lebih dalam ke dalam misteri matematika dan menggunakannya sebagai alat untuk menyederhanakan perhitungan yang kompleks.

Oleh karena itu, bilangan pangkat adalah pintu keajaiban matematika yang dapat membantu kita menjelajahi dunia ilmu pengetahuan dengan lebih baik.

Rumus Bilangan Pangkat Kelas 10

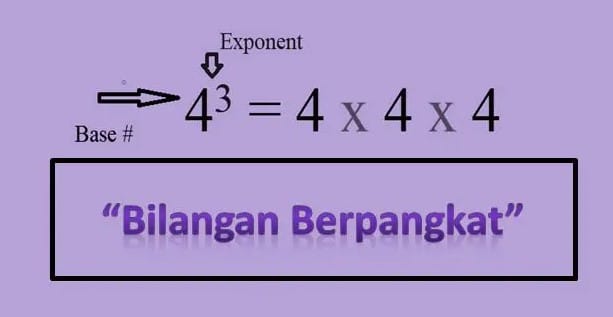
Konsep bilangan pangkat atau eksponen adalah dasar yang kuat dalam matematika, dan rumus umumnya adalah kunci untuk memahami bagaimana bilangan-bilangan ini berinteraksi.

Mari kita perluas pemahaman kita tentang rumus umum bilangan pangkat. Rumus umumnya dapat dirumuskan sebagai berikut:

a^b

Namun, terdapat beberapa catatan penting:

Nilai Basis (a): Basis adalah bilangan yang menjadi dasar dari perhitungan. Penting untuk dicatat bahwa basis tidak boleh bernilai satu, karena apapun pangkat yang digunakan pada bilangan satu, hasilnya akan selalu tetap satu.
Nilai Pangkat (b): Pangkat (eksponen) adalah bilangan yang menentukan berapa kali basis akan dikalikan dengan dirinya sendiri. Pangkat bisa berupa angka real, seperti 2, 4, 5, -3, -2, dan lainnya.

Dalam rumus ini, basis dan pangkat memiliki peran yang sangat penting dalam menentukan hasil perhitungan. Basis adalah “bilangan pokok” yang kita “tingkatkan” sebanyak b kali sesuai dengan eksponen.

Rumus ini adalah landasan untuk berbagai perhitungan matematika yang lebih kompleks.

Pemahaman yang kuat tentang rumus umum bilangan pangkat akan membantu kita menjelajahi berbagai konsep matematika lebih lanjut, seperti perpangkatan dengan bilangan pecahan, eksponen negatif, dan eksponen pecahan.

Ini adalah fondasi yang solid untuk memahami dunia matematika yang penuh dengan keajaiban dan penemuan.

Jenis-Jenis Bilangan Berpangkat yang Harus Kamu Ketahui!

Dalam dunia matematika, bilangan pangkat memiliki berbagai variasi yang menarik, dan masing-masing memiliki sifat dan aturan yang unik.

Mari kita menjelajahi empat jenis utama dari bilangan berpangkat beserta contohnya yang dapat memperkaya pemahaman kita.

Bilangan Pangkat Positif

Jenis pertama adalah bilangan pangkat positif, di mana eksponen atau pangkatnya adalah angka positif. Rumus umumnya adalah: a^n = a x a x a x … x a Dalam rumus ini, ‘a’ adalah basis (bilangan pokok), dan ‘n’ adalah pangkat. Contoh:

2^3 = 2 x 2 x 2 = 8 Dari contoh di atas, kita dapat melihat bahwa semakin besar pangkatnya, semakin besar pula nilai bilangan tersebut.

Bilangan Pangkat Negatif

Berbeda dengan yang pertama, bilangan pangkat negatif memiliki eksponen yang negatif. Rumus umumnya adalah: a^(-n) = 1 / (a^n) Di sini, ‘a’ adalah bilangan riil yang bukan nol, dan ‘n’ adalah bilangan bulat positif. Contoh:

3^(-2) = 1 / (3^2) = 1 / 9 Pada jenis ini, semakin besar pangkat negatifnya, semakin kecil nilai bilangan tersebut.

Bilangan Pangkat Nol

Bilangan pangkat nol memiliki eksponen nol. Rumusnya adalah: a^0 = 1 Dalam hal ini, ‘a’ harus bukan nol. Contoh:

5^0 = 1 Nilai bilangan pangkat nol selalu sama, yaitu 1.

Bilangan Pangkat Pecahan

Terakhir, kita memiliki bilangan pangkat pecahan, di mana eksponennya berupa pecahan. Rumusnya adalah: a^(m/n) = (akar(n) dari a)^m Di sini, ‘a’ adalah bilangan riil positif, ‘m’ adalah pembilang, dan ‘n’ adalah penyebut. Contoh:

4^(1/2) = √4 = 2 Pada jenis ini, kita menggunakan akar n-te dari bilangan ‘a’ dan mengangkatnya ke pangkat ‘m’.

Dengan pemahaman tentang berbagai jenis bilangan pangkat ini, kita dapat lebih luas dalam menjelajahi matematika dan menerapkannya dalam berbagai konteks perhitungan yang berbeda.

Sifat-sifat Bilangan Berpangkat dan Bentuk Akar

Dalam dunia matematika, pemahaman tentang sifat-sifat bilangan berpangkat sangat penting teman-temman COVIDCARE.

Sifat-sifat ini menjadi dasar dalam operasi dan perhitungan menggunakan eksponen. Mari kita teliti lebih lanjut sifat-sifat yang relevan ini:

Sifat Penjumlahan Pangkat

Ketika kamu memiliki perkalian dari dua atau lebih bilangan pangkat dengan basis yang sama, kamu bisa menerapkan sifat penjumlahan pangkat.

Ini berarti jika bilangan pangkat dengan basis yang sama dikalikan, maka kamu dapat menjumlahkan pangkatnya. ab x ac = ab+c Contoh:

2^3 x 2^2 = 2^(3+2) = 2^5
2^3 x 2^4 x 2^2 = 2^(3+4+2) = 2^9 Sifat ini hanya berlaku jika basis atau bilangan pokoknya sama.

Sifat Pengurangan Pangkat

Konsep ini mirip dengan sifat penjumlahan pangkat, tetapi berlaku untuk pembagian bilangan pangkat dengan basis yang sama.

Jadi, jika bilangan pangkat dengan basis yang sama dibagi, kamu dapat mengurangkan pangkatnya. ab / ac = ab-c Sama seperti sifat penjumlahan, ini hanya berlaku jika basisnya sama.

Sifat Perpangkatan Bilangan Berpangkat

Ketika kamu memiliki eksponen yang dipangkatkan, dan hasilnya dipangkatkan lagi, kamu dapat mengalikan pangkat-pangkat tersebut. (a^b)^c = a^(b*c) Contoh:

(2^3)^2 = 2^(3*2) = 2^6
(3^2)^3 = 3^(2*3) = 3^6 Sifat ini memungkinkan untuk mengekspresikan operasi berulang dalam pangkat.

Sifat Bilangan Pangkat Nol

Ketika suatu bilangan dipangkatkan dengan 0, hasilnya selalu 1, asalkan basisnya tidak nol. a^0 = 1 (jika a ≠ 0) Contoh:

2^0 = 1
5^0 = 1 Sifat ini berguna dalam perhitungan matematika yang melibatkan eksponen.

Sifat-sifat ini adalah dasar dalam memahami dan menerapkan bilangan berpangkat dalam berbagai konteks matematika. Dengan memahami sifat-sifat ini, kamu dapat melakukan perhitungan dengan lebih baik dan efisien.

Sifat Perkalian Pangkat

Sifat ini berlaku ketika bilangan berpangkat dipangkatkan kembali. Dengan kata lain, jika kamu memiliki bilangan yang dipangkatkan dan hasilnya dipangkatkan lagi, maka kamu dapat mengalikan pangkat-pangkat tersebut.

(ab)^c = a^c x b^c

Contoh:

(2^5)^3 = 2^(5*3) = 2^15
(3^2)^4 = 3^(2*4) = 3^8 Sifat perkalian pangkat juga berlaku ketika kamu mengalikan dua bilangan berpangkat yang memiliki basis dan pangkat yang sama. Contoh:
(5^5) x (5^2) = 5^(5+2) = 5^7 Namun, jika basisnya sama tetapi pangkatnya berbeda, kamu tidak dapat mengaplikasikan sifat ini dan perlu menggunakan sifat penjumlahan pangkat.

Sifat Pembagian Pangkat

Sifat ini berkaitan dengan operasi akar dalam bentuk bilangan berpangkat. Ketika kamu mengubah operasi akar menjadi bentuk eksponen, maka kamu bisa menerapkan sifat pembagian pada pangkat.

Namun, yang perlu diperhatikan adalah yang dibagi adalah pangkat, bukan basisnya. a^(m/n) = (a^m)^(1/n) = √(a^m) Contoh:

2^(3/2) = (2^3)^(1/2) = √(2^3) = √8
4^(2/3) = (4^2)^(1/3) = √(4^2) = √16 Sifat ini memungkinkan untuk mengekspresikan operasi akar dalam bentuk eksponen, yang dapat mempermudah perhitungan.

Dengan pemahaman yang baik tentang sifat-sifat bilangan berpangkat ini, kamu dapat lebih efisien dalam menjalankan operasi dan perhitungan yang melibatkan eksponen.

Sifat Pangkat Satu

Angka 1 memiliki peran khusus dalam operasi matematika. Dalam konteks perpangkatan, ketika suatu bilangan dipangkatkan 1, hasilnya selalu sama dengan bilangan itu sendiri.

Ini karena perpangkatan adalah bentuk perkalian berulang, dan ketika angka 1 digunakan sebagai pangkat, hanya ada satu kali perkalian yang terjadi, yaitu dengan bilangan itu sendiri. a^1 = a Contoh:

2^1 = 2
3^1 = 3
100^1 = 100 Dengan kata lain, berapapun bilangan pokoknya, jika dipangkatkan 1, hasilnya tetap sama dengan bilangan itu sendiri.

Sifat Pangkat Negatif

Bilangan pangkat negatif adalah konsep yang memungkinkan dalam matematika. Sifat ini mengubah bilangan berpangkat negatif menjadi pecahan, di mana pembilangnya adalah 1 dan penyebutnya adalah basisnya yang dipangkatkan positif. a^(-b) = 1 / (a^b) Contoh:

2^(-3) = 1 / (2^3) = 1/8
5^(-2) = 1 / (5^2) = 1/25
10^(-1) = 1 / (10^1) = 1/10

Sifat pangkat negatif mengubah bilangan berpangkat negatif menjadi bilangan pecahan dengan pembilang 1 dan penyebut yang sesuai.

Contoh Soal Bilangan Berpangkat dan Jawabannya

Contoh Soal 1

Tentukan nilai (y) yang memenuhi persamaan (6^{2y-4} = 36^3).

Pembahasan:

Untuk menentukan nilai (y), kita perlu menyamakan kedua sisi persamaan dengan basis yang sama. Karena (36) adalah hasil dari (6^2), kita dapat menyusun ulang persamaan sebagai berikut:

6^{2y-4} = (6^2)^3

Selanjutnya, kita tahu bahwa ((6^2)^3 = 6^{2 \cdot 3} = 6^6). Jadi, kita memiliki persamaan:

6^{2y-4} = 6^6

Karena basisnya sama, maka eksponennya juga harus sama:

2y-4 = 6

Sekarang kita selesaikan untuk (y):

2y = 6 + 4

2y = 10

y = \frac{10}{2}

y = 5

Jadi, nilai (y) yang memenuhi persamaan adalah (5).

Contoh Soal 2

Berapa hasil dari operasi ( (-5)^3 + (-5)^2 + (-5)^1 + 50)?

Pembahasan:

Kita dapat menghitung setiap suku dari operasi ini secara terpisah:

(-5)^3 = (-5) \times (-5) \times (-5) = -125

(-5)^2 = (-5) \times (-5) = 25

(-5)^1 = -5

50 = 1

Sekarang kita jumlahkan semua suku tersebut:

-125 + 25 – 5 + 1 = -104

Jadi, hasil dari operasi tersebut adalah (-104).

Dengan pemahaman tentang pengertian, jenis, sifat, dan contoh-contoh bilangan berpangkat, teman-teman COVIDCARE akan lebih siap untuk menyelesaikan berbagai masalah matematika yang melibatkan perpangkatan. Selamat belajar!

Baca juga: